
Soft matter, focussing on hydrogels and their interactions with phospholipid membranes, nanoparticles, nano-emulsion droplets, and micro-bubbles. We use electroacoustic diagnostics, conductivity, dielectric spectroscopy, rheology, light-scattering, and optical microscopy, including theoretical models to advance technologies impacting human health and the environment.
Samples above courtesy of J. Wu (left) and A. Nassirian (right). All rights reserved.
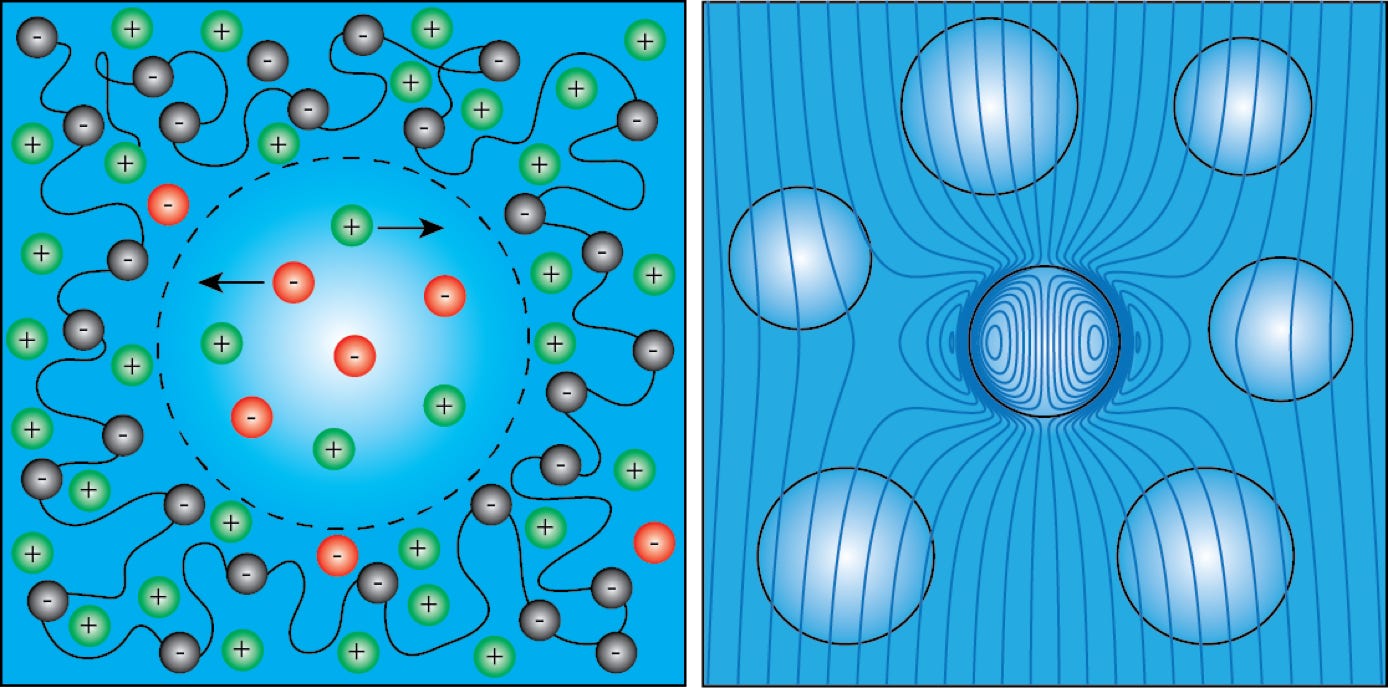
Theoretical calculations of the hydrodynamic permeability and electrical conductivity of cavity-doped hydrogels (Hill, J. Fluid Mech., 2022). The figure on the right shows the electrostatic potential disturbance of a single cavity in a charged hydrogel. This reflects electro-migration, diffusion and electroosmotic advection in the gel and cavity phases. The theory provides the averaged flux produced by averaged gradients of electrostatic potential (electric field) and pressure, consistent with Onsager reciprocity, thus accommodating a variety of experimental electrode configurations.
ELECTROKINETIC PHENOMENA
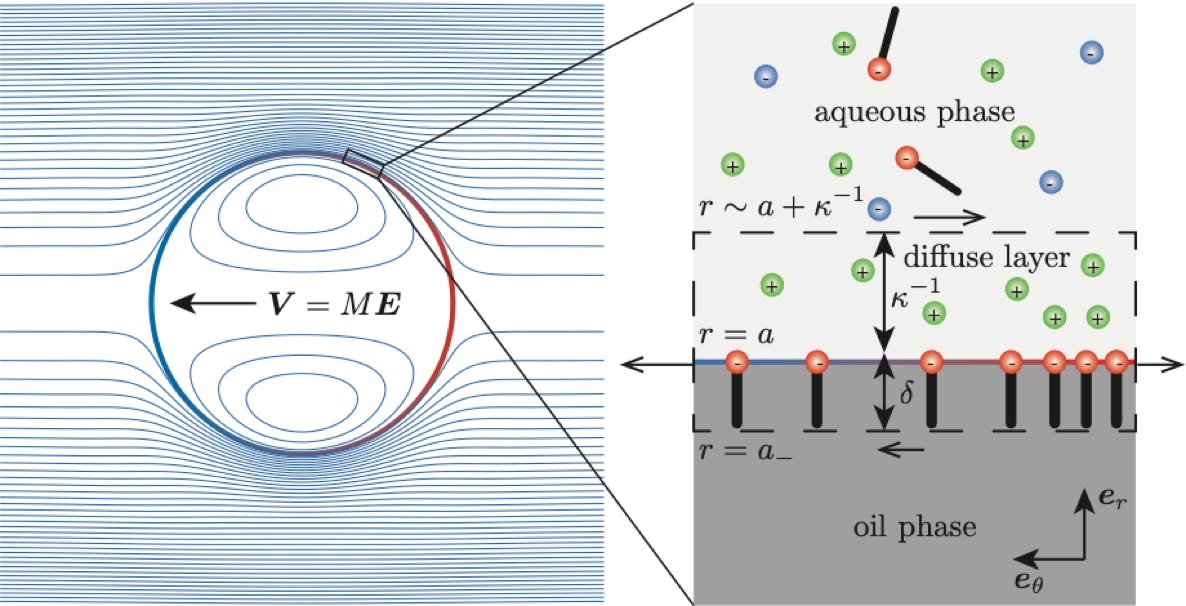
“Dynamic electrophoretic mobility of surfactant-stabilized nano-droplets” (R. J. Hill & G. Afuwape, J. Fluid Mech., 2020). This paper provides an analytical solution of an electrokinetic model for nano-emulsion droplets: large, highly charged droplets, at the high-frequencies encountered in ESA and DRS instruments. This model unifies interfacial equilibrium thermodynamics (from pendant-drop surface-tension experiments) and electrokinetics (from the electro-kinetic-sonic amplitude), as measured in our laboratory by G. Afuwape. The theory is now being used to measure the size of nano-drops trapped in gels at high density, using the electro-kinetic-sonic amplitude. These data and their theoretical interpretation also furnish rheological spectra at MHz frequencies. See more recent publications (2021) for details of the isotherm (J. Phys. Chem. C), and applications to emulsion-doped hydrogels for drug-delivery applications (ACS Applied Polymer Materials).

“Electrokinetic spectra of dilute surfactant-stabilized nano-emulsions” (R. J. Hill, J. Fluid Mech., 2020). This paper studies exact/computational solutions of the electrokinetic model for nano-emulsion droplets: any size, surface charge and frequency. The figures here show the (external) translation- and electric-field-induced flows, and the flow prevailing under free dynamic electrophoresis (blue and red are the real and imaginary parts of the flow). See animations below for temporal reconstructions.
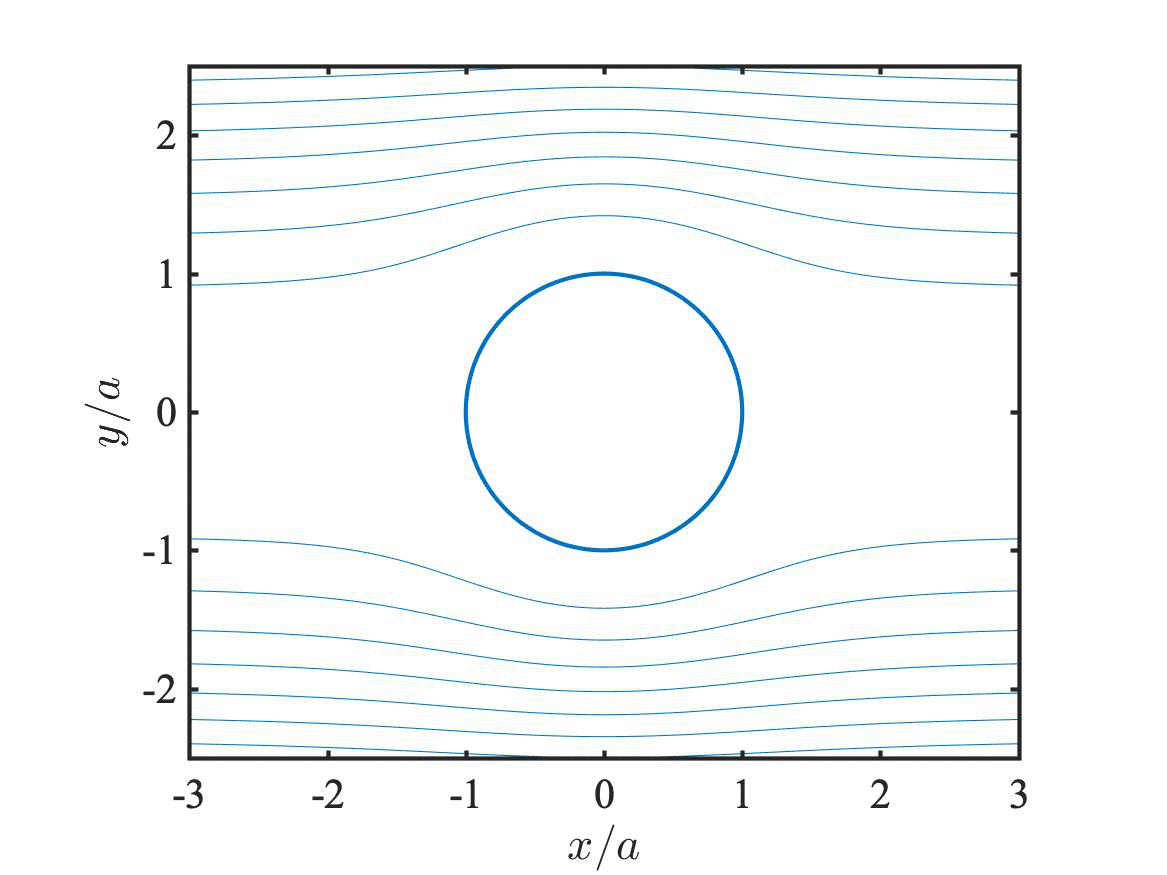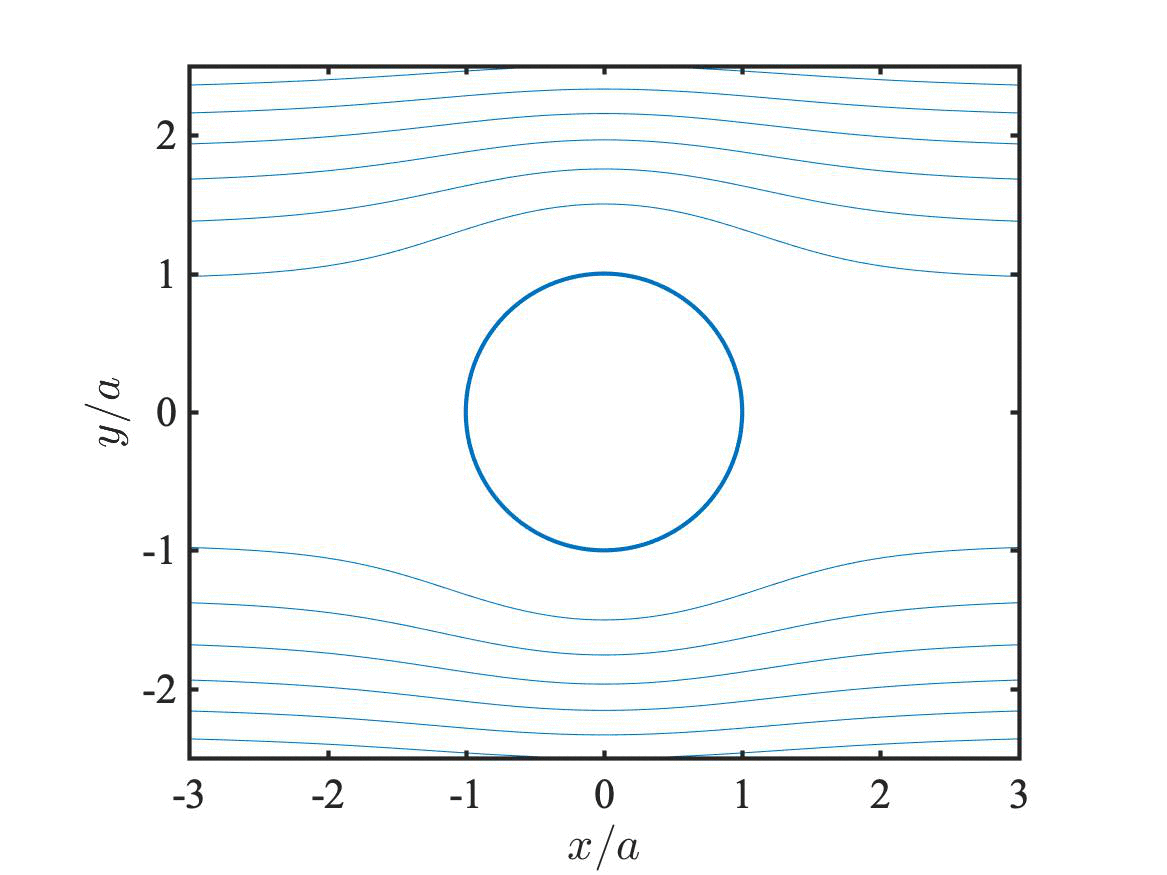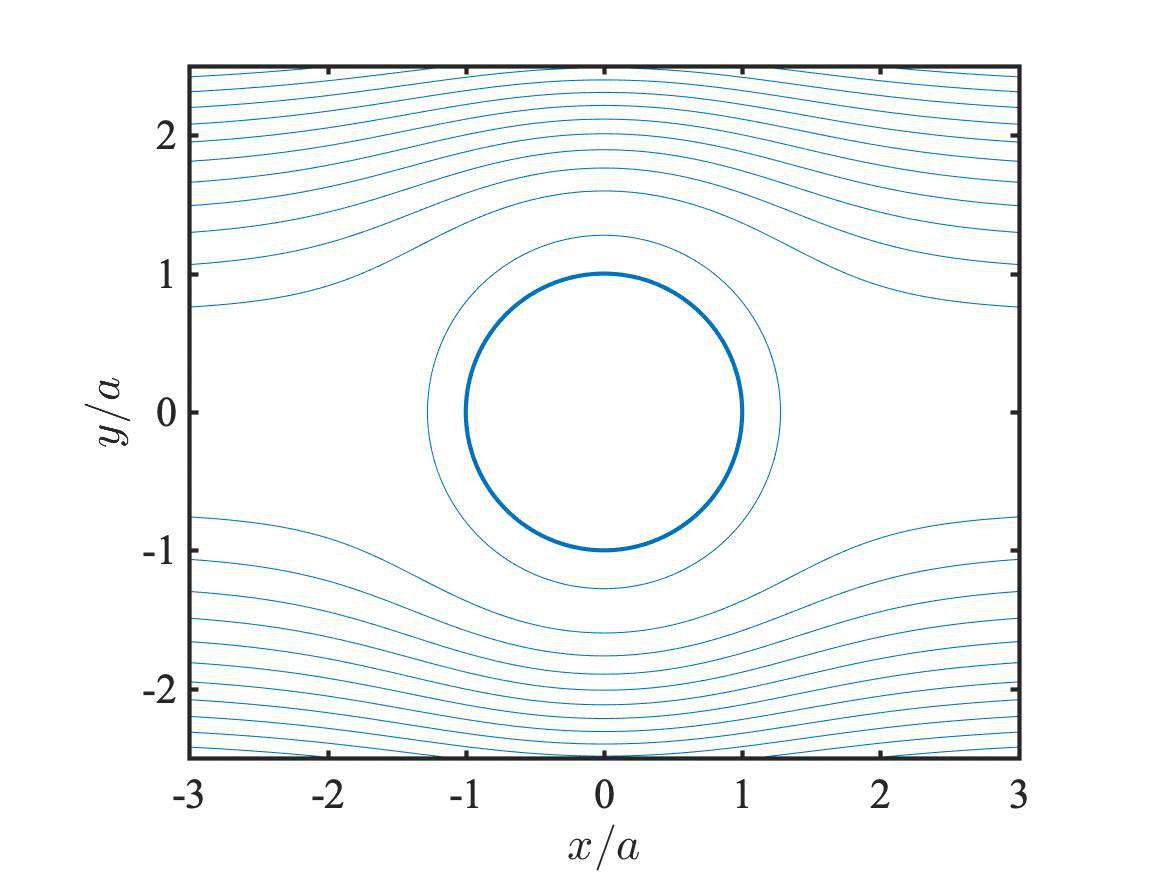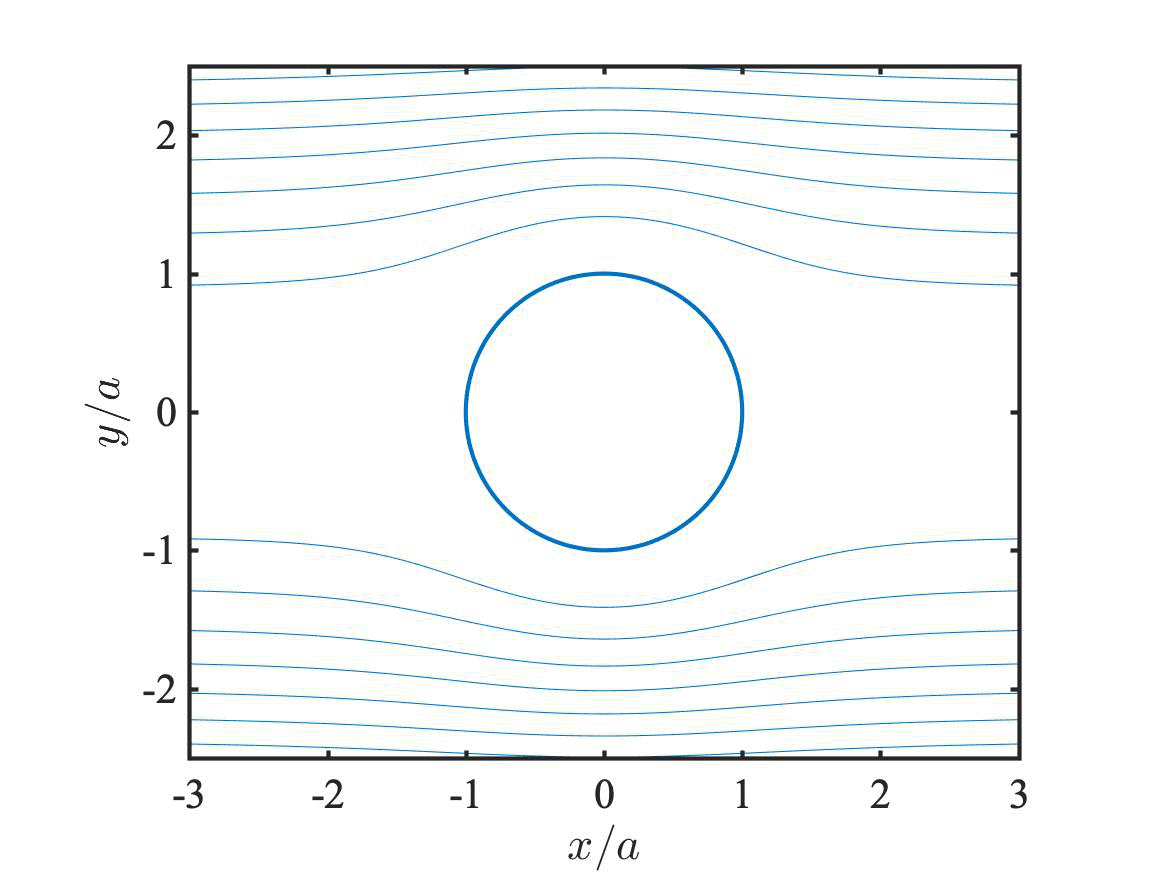
Streamlines of the U- (top left), E- (top right), and M- (bottom) problems above, animated for one complete period of oscillation at 10 MHz. (Thanks to D. J. Hill for assistance with Imagemagick). These sequences are constructed from the analytical-approximate solution of R. J. Hill & G. Afuwape, J. Fluid Mech., 2020. The flows nicely demonstrate the role of temporal inertia at zero Reynolds number. Note the flow and/or electric-field reversal (e.g., at one and three quarters of the period), first manifesting at the oil-water interface, where the interfacial charge and diffuse-layer charge reside.
HYDROGELS AND NANO-COMPOSITES

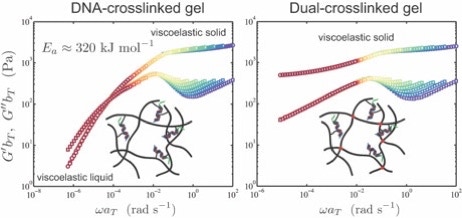
Time-temperature-superposition rheological analysis of DNA-cross-linked hydrogels (C. Du & R. J. Hill, Macromolecules, 2019)
BIOLOGICAL MEMBRANES
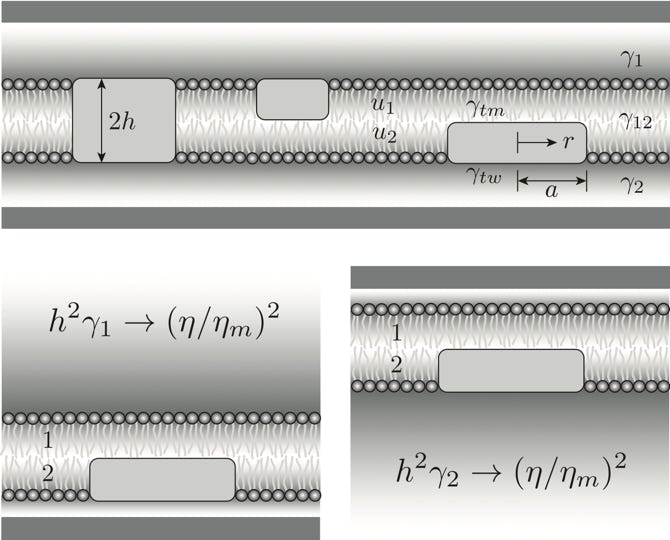
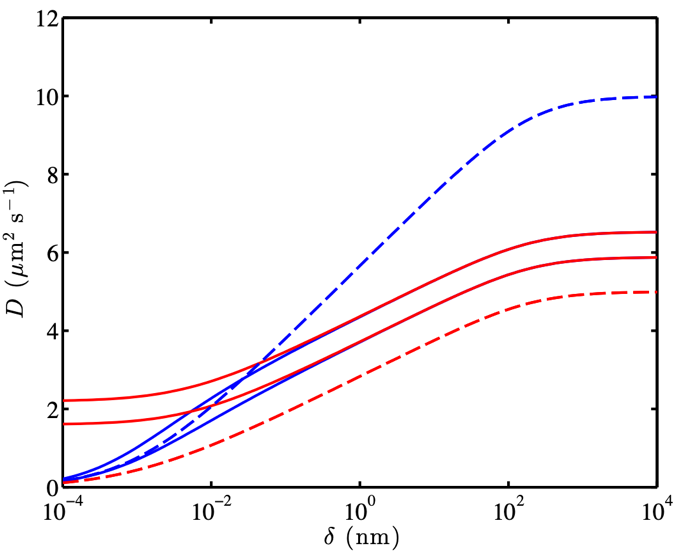
Tracer diffusion in supported phospholipid bilayer membranes (C.-Y. Wang & R. J. Hill, Proc. R. Soc. A, 2014)
NANOSTRUCTURED POROUS MEDIA
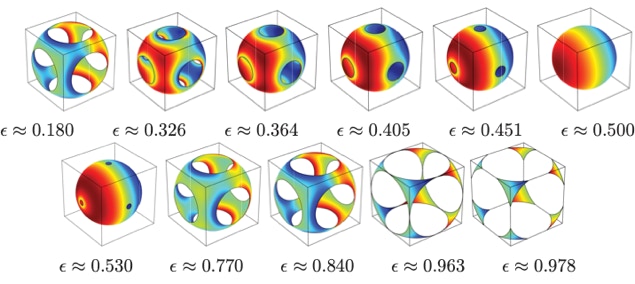
Unified interfacial thermodynamics and diffusion in nanoporous media (M. Mirbagheri & R. J. Hill, Chem. Eng. Sci., 2017)
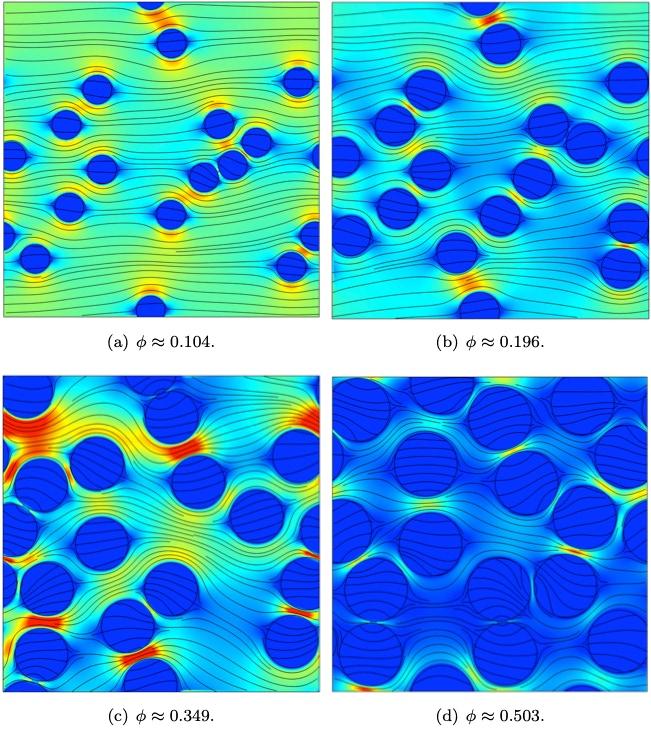
Cavity-doped hydrogels (R. J. Hill, J. Fluid Mech., 2023): An analytical theory for the hydrodynamic permeability is compared to direct computations in ordered and random arrays over a wide range of inclusion volume fractions.
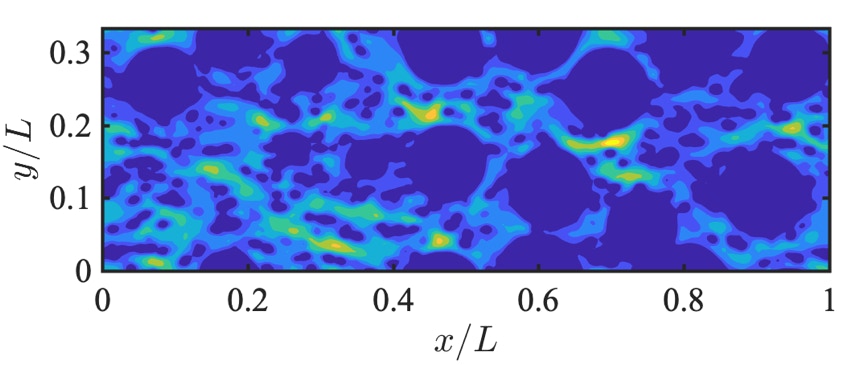
Direct computations (using the lattice-Boltzmann method) of Stokes flows in a bi-disperse random array of impenetrable spheres:
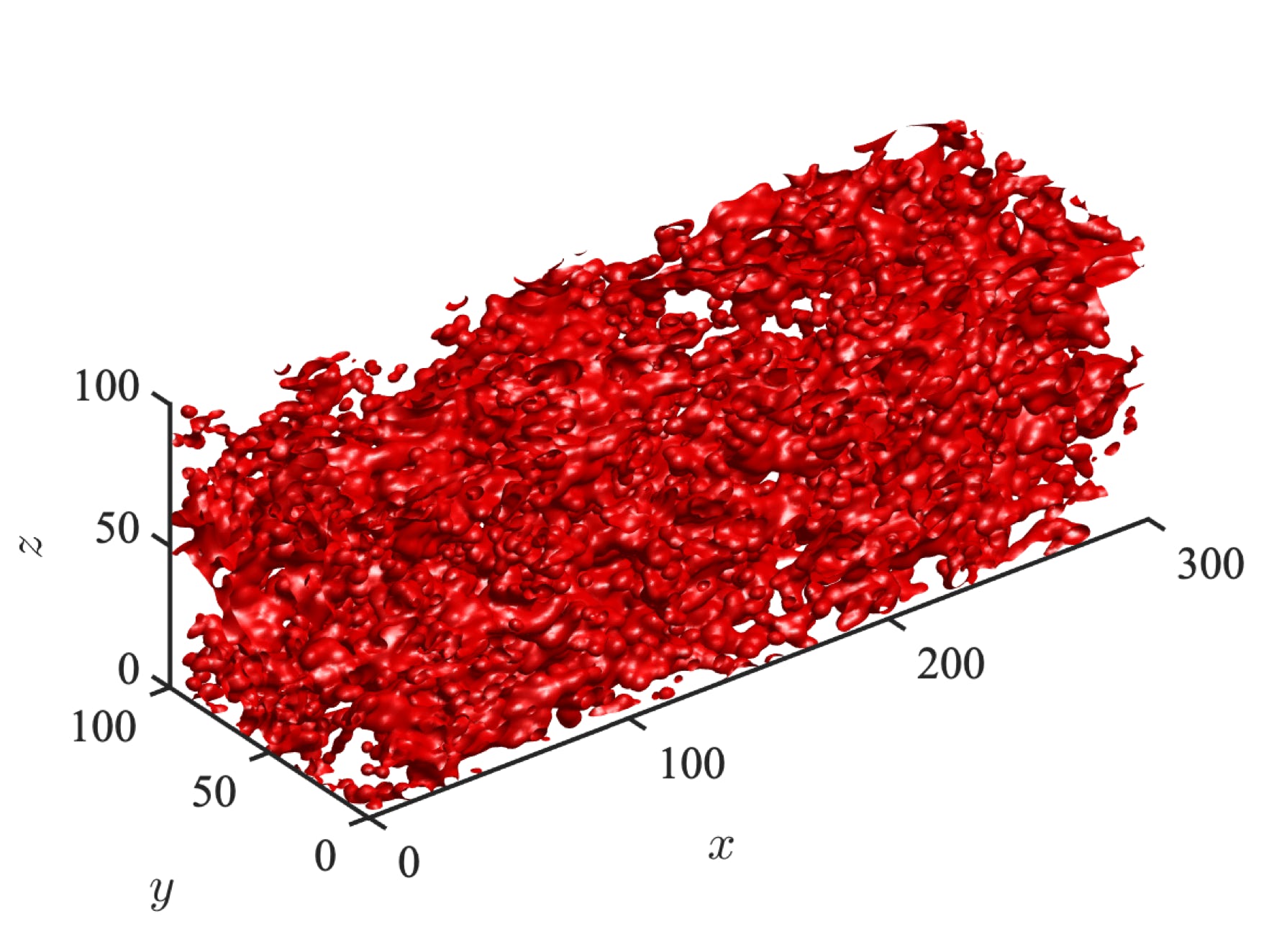
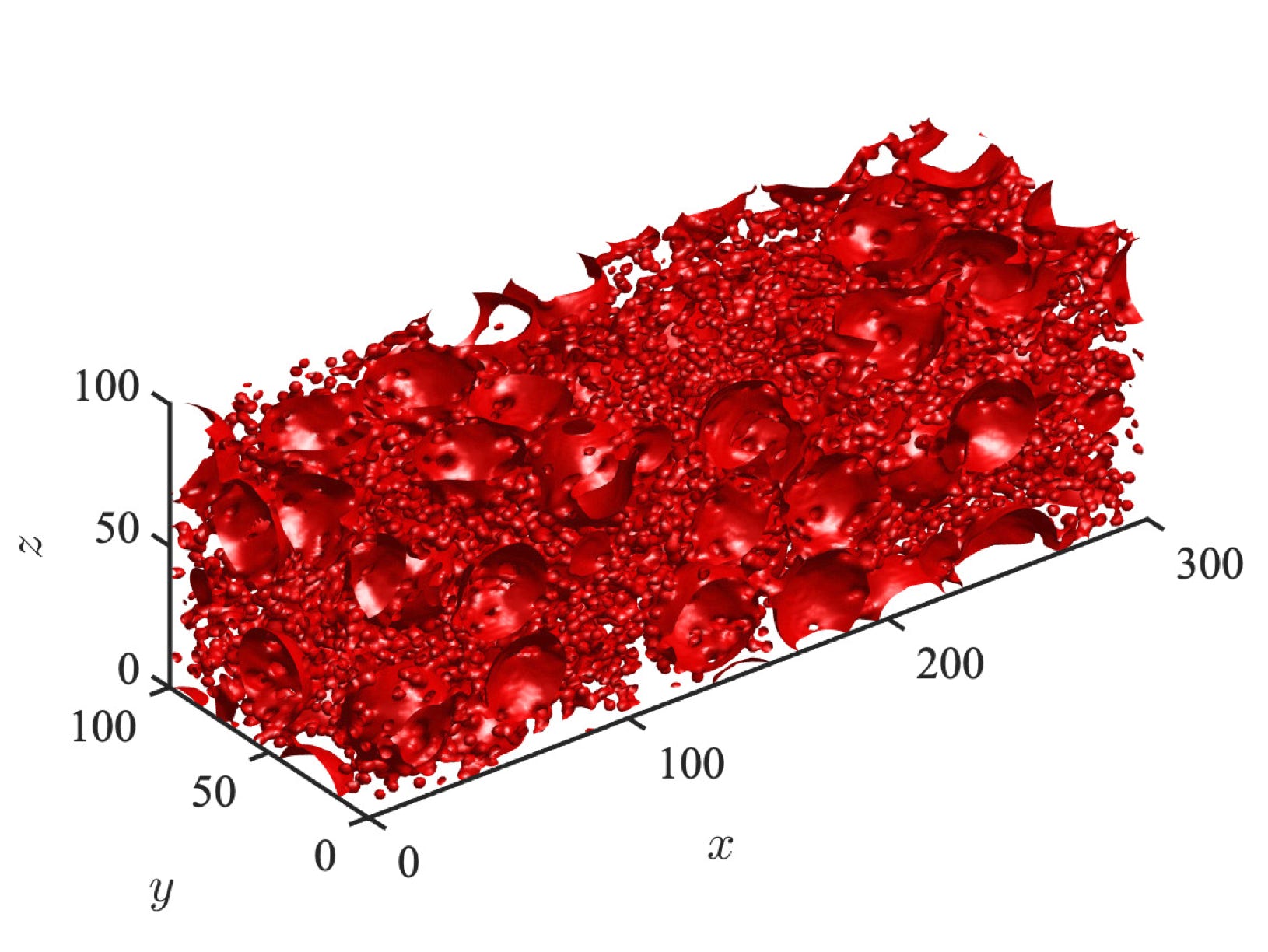
Direct computations (using the lattice-Boltzmann method) of Stokes flows in a random array of impenetrable spheres with spherical cavities: